信息奥赛志愿服务活动20181104上午
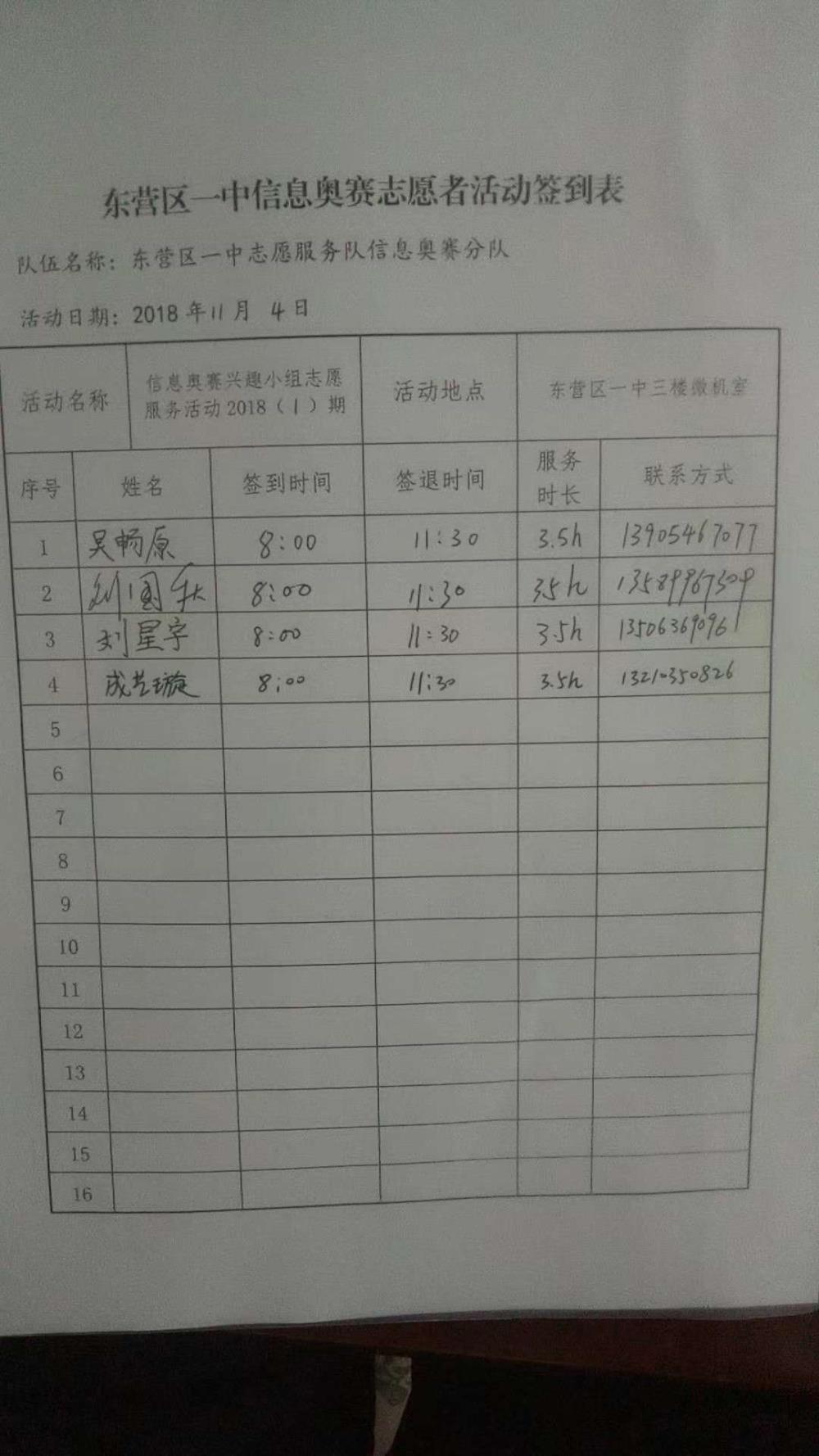
| 编号 | 2018045291 | 服务区域 | 胜利街道 |
| 服务地点 | 东营区一中三楼微机室 | 所属团体 | 东营区第一中学志愿服务队 |
| 联系人 | 刘* | 联系电话 | 1358996**** 729**** |
| 服务时长 | 3.5小时 | 活动日期 | 2018-11-04 08:00:00 至 2018-11-04 11:30:00 |
信息奥赛志愿服务活动20181104上午 刘国庆是东营区一中中学部一名信息技术老师,有着扎实的业务功底和多年的信息奥赛辅导经验,作为一名志愿者,凭借爱好和热心,自2006年至今义务辅导学生累计200余人,学生参加全国青少年信息学奥林匹克联赛,年年获国家省市一二等奖。个人被评为全国信息学奥赛优秀辅导教师、山东省奥赛辅导先进工作者。今年,信息奥赛兴趣小组成员有35人,每周二晚18:30—20:00,每周日下午14:30—17:30集体活动。志愿者吴畅原、李星宇、成艺璇积极参与其中。11月4日上午上午讲解背包问题。问题: 有N件物品和一个容量为V的背包。第i件物品的费用(即体积,下同)是w[i],价值是c[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。 基本思路: 这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。 用子问题定义状态:即f[i][v]表示前i件物品(部分或全部)恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是:f[i][v]=max{f[i-1][v],f[i-1][v-w[i]]+c[i]}。 这个方程非常重要,基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下:“将前i件物品放入容量为v的背包中”这个子问题,若只考虑第i件物品的策略(放或不放),那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品,那么问题就转化为“前i-1件物品放入容量为v的背包中”;如果放第i件物品,那么问题就转化为“前i-1件物品放入剩下的容量为v-w[i]的背包中”,此时能获得的最大价值就是f [i-1][v-w[i]]再加上通过放入第i件物品获得的价值c[i]。 活动组织总结刘国庆+1小时,图片资料上传成艺璇+1小时